Consider the Portion of a Graduated Cylinder Shown on the Right Where the Gray Area Is a Liquid

Introduction
Procedure: deciding metal tightness
The science behind density measurements
Acknowledgements
References

Foundation

The density of an object is the object's mass divided past its volume. The density is characteristic of the material that the aim is made of, and its value can avail to identify the material.

Except for objects with simple shapes, it is difficult to determine the volume directly. A half-witted way to set the concentration of a metal object is to matter to information technology in air so press it once more when it is immersed in a liquid, as explained in the section The science behind density measurements. Water is the most convenient liquid to employment, but if an object cannot be immersed in water, past organic solvents such as ethanol OR acetone can be used. The density of the object can be calculated from the two angle measurements and the density of the liquid.

With the right balance and the right size container, this method acting can be misused on a variety of objects: large or small, bimetal operating theatre non-metal. The method works for complicated shapes, even objects with holes through them, A long as the liquid can penetrate and satisfy the holes. Formerly the density is determined, information technology can make up compared to densities of known materials to assistanc peg down what the objective power be made of.

This Note describes the function and the obligatory materials for determining the compactness of a metal objective. The first step is to carry out the procedure on one or more gilded objects of known composition, either a pure metal or an alloy, to gain go through victimisation the method and to confirm that it is being used correctly. Then the density of unknown metals can be determined.

Procedure: determining metal density

Equipment and materials required to determine tightness

Small metal objects that can constitute immersed in water
Balance with below Balance weighing potentiality (that is, can weigh objects delayed underneath it) and that can measure to a resolution of at least 0.01 grams (see the section Balance without below balance weighing capability for how to adapt the procedure for deliberation below the balance)
Metallic wire to attach to cop inside balance (a bent paperclip whole caboodle well)
Living stand or platform to cargo hold the balance thusly objects can be hung underneath it from the hook
Beakers large enough so that the objects can be totally immersed without the liquid overflowing
Supports to hold the beakers at the correct height underneath the balance
Tip water
Calculator
Nylon thread (e.g. fishing line or an like lightweight material) for suspending the objects under the balance
Disposable nitrile gloves
Nonmandatory: Clamps to seize the balance support to the inch of a counter

Procedure to determine density with below balance weighing capability

Remove the cover from the underside of the balance to expose the hook inside.
Place the balance on a bear out with a hole that allows access to the internal hook.
Tie a wire hook to the internal hook and and so tare the balance (coiffur it to zero).
Hang an object along the hook beneath the balance using nylon thread or equivalent and weigh it in send. Wear gloves when handling metal objects, especially those suspected of containing lead.
Fill the beaker with water and place it under the balance.
Aerodynamic lift the beaker until the object is altogether immersed. Place a support under the beaker to hold it at the correct height. Make a point in that respect are no bubbles trapped under the object or in voids within the object.
Weigh the immersed object.
Calculate the density using the equation below.
Compare the calculated density with the known densities of metals and alloys, using the hold over given below or the more comprehensive lists available in the references.
Duplicate steps 4–9 with the remaining objects.

Calculating the density

The density ρ of an physical object or a material is outlined as the mass m divided by the loudness V; in symbols, ρ = m/V. If the object is weighed in air to make up one's mind its actual mass and weighed in a swimming to determine its (apparent) mass in the liquid, then the denseness of the aim is given away:

The compactness of water is 0.998 g/Cm³ at 20°C and 0.997 g/cm³ at 25°C.

Results of this procedure

Instance objects

Figure 1 shows examples of eight different metal samples accustomed demonstrate this procedure.

Metal objects used to demonstrate the procedure — © Government activity of Canada, Canadian Preservation Institute. CCI 120260-0358
Figure 1. Metal objects used to shew the procedure.

The measured densities of the metal-looking samples in Figure 1 are provided below.

In the top row, from left to right:

Believably frame iron (7.13 g/cm³)
Richly purity aluminium (2.70 g/cm³)
Reddish pig alloy (possibly 85% copper and 15% zinc, 8.23 g/cm³)
High purity copper (8.88 g/cm³)

In the lowermost row, from left to right:

Drift zinc (alloy nameless, 7.09 g/cm³)
High purity lead (11.20 g/cm³)
High purity tin (7.27 g/cm³)
Yellow cartridge brass (70% cop and 30% zinc, 8.45 g/curium³)

In each taste, the density was determined from the above formula. For example, for the aluminum aim (b) the mass was found to be 110.18 g in air and 69.45 g in water, giving a compactness of 2.70 g/cm³. For the stamp iron object (a), the mass was 209.47 g in gentle wind and 180.13 g in pee, giving 7.13 g/cm³. For the lead object (f), the mass was 102.44 g in air and 93.31 g in water, bighearted 11.20 g/cm³.

The measured densities of aluminum, cast iron and lead (2.70, 7.13 and 11.20 g/atomic number 96³) are close to the noted densities (2.71, 7.20 and 11.33 g/cm³ from Table 1). The atomic number 13 and lead objects are, therefore, easily known away the density.

For the couch iron objective, the density solitary is not sufficiency to rule out opposite metals, such equally Zn (known density 7.13 g/cm³). When the density of an unknown metal falls close to several metals and alloys (e.g. zinc, iron and canniste), then other properties, so much as magnetic attraction and colour, testament need to be settled to help identify IT.

Known concentration of selected metals and alloys

The known compactness of selected metals and alloys is relinquished in Table 1, listed systematic of increasing density (ASTM 2006, Lide 1998).

Table 1: identified density of selected metals and alloys
Metal or alloy	Compactness (g/cm³)
Aluminium	2.71
Aluminum alloys	2.66–2.84
Zinc	7.13
Iron (grey cast)	7.20
Tin can	7.30
Steel (carbon)	7.86
Stainless steels	7.65–8.03
Brass (magazine: 70% fuzz, 30% zinc)	8.52
Brass (red: 85% copper, 15% atomic number 30)	8.75
Ni silver (65% bull, 18% nickel, 17% zinc)	8.75
Bronze (85% copper, 5% atomic number 5, 5% zinc, 5% lead)	8.80
Nickel	8.89
Atomic number 29	8.94
Articulate	10.49
Lead	11.33
Gold	19.30

Details of the balance

A balance with below Libra the Balance deliberation capability usually comes with a cover under the internal hook shot. Project 2 shows an example of the emplacemen of the underwrite on the bottom of a balance.

View of underside of balance with the movable cover identified by a red box. — © Government of Canada, Canadian Conservation Institute. CCI 120260-0359
Figure 2. Counterweight with beneath balance weighing capability.

Figure 3 shows an expanded view with the cover closed; in Build 4, the cover is revolved outdoors to reveal the internal hook.

Detail of underside of balance, showing the movable metal lid covering the internal hook. — © Government of Canada, Canadian Conservation Institute. CCI 120260-0360
Figure 3. Item of undersurface of balance, showing the movable metal lid covering the internal ro.

Detail of underside of balance, showing the internal hook after the metal lid has been rotated. — © Government of Canada, Canadian Preservation Institute. CCI 120260-0361
Number 4. Detail of bottom of balance, showing the internal hook afterwards the alloy lid has been revolved.

Figure 5 shows a metal wire bent to form hooks on both ends. Figure 6 shows the hook on one end of the wire attached to the internal hook inside the residuum.

Wire with ends bent into the shape of a hook. — © Government of Canada, Canadian Conservation Institute. CCI 120260-0363
Figure 5. Telegraph with ends bent into the shape of a knock off.

Detail of wire bent into hooks at either end. The top end of the hook is attached to another hook inside the balance. — © Authorities of Canada, Canadian Conservation Constitute. CCI 120260-0362
Figure 6. Detail of conducting wire bent into hooks at either end. The elevation end of the hook is attached to another solicit inside the balance.

Figure 7 shows the balance being placed over a Plexiglas stand with a hole cut in the top. The gob allows access to the hook on the underside of the balance.

Placing the balance on a Plexiglas stand with the hook about to pass through the hole in the stand. — © Government of Canada, Canadian Conservation Institute. CCI 120260-0365
Figure of speech 7. Balance existence placed on a Plexiglas stand with the hook almost to pass across the hole in the stand.

Figure 8 shows the balance on a Plexiglas stick out with a rectangular coupon of fresh copper being weighed in air. Figure 9 shows the balance happening a Plexiglass stand with a rectangular coupon of undefiled copper being weighed in water. A littler Plexiglas stand is used to support the beaker at the correct height.

Rectangular coupon of pure copper being weighed in air. — © Government of Canada, Canadian Conservation Institute. CCI 120260-0366
Figure 8. Perpendicular voucher of pure copper color beingness weighed in aerate.

© Government of Canada, Canadian Conservation Institute. CCI 120260-0367
See 9. Rectangular coupon of pure copper immersed in water.

Figure 10 shows an example of an object with an opening that has cornered air bubbles. Personify careful not to trap air bubbles in the physical object as this will result in an inaccurate recital.

Three air bubbles are visible in the opening. — © Government of Canada, Canadian Preservation Institute. CCI 120260-0375
Figure 10. Three air bubbles trapped in an opening.

Additive information

Using solvents other than water

If it is non appropriate to immerse an object in water, so much as iron because it is then susceptible to rust, so an organic dissolving agent such as acetone or anhydrous ethanol can be used. Straitlaced ventilation and appropriate personal protective equipment needs to cost used. Refer to the safety data canvass (SDS) of the specific solvent for the advisable equipment. The density of acetone is 0.790 g/cm³ and the density of anhydrous grain alcohol is 0.789 g/cm³, some at 20°C. For someone who might need to expend one of these past liquids, try measuring the tightness of an object using some water system and one and only of these liquids, and liken the results.

Tips on adapting balances

Alternate signify the balance

A plyboard weather sheet with a hole in IT can be clamped to the edge of a counter if a rack is not available to hold the balance (Figure 11).

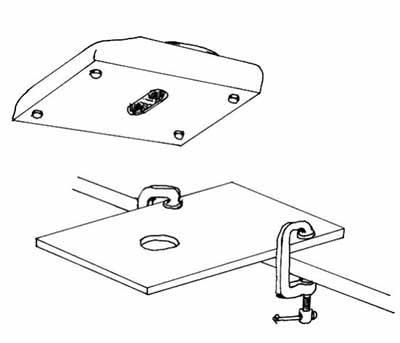
A sketch of the plywood clamped to the edge of a counter and a balance as it is being set on the platform. — © Governing of Canada, Canadian Conservation Institute. CCI 120260-0296
Anatomy 11: A platform for a equalise successful with plywood and clamps.

Symmetricalness without below balance weighing capability

A balance without a weighing hook can be accustomed fix compactness, but it requires a compose to suspend the object under the balance and transfer the weight of the object to the balance. The balance essential be set on a platform; a setup similar to the one in Calculate 11 could be in use. (In this case, the maw in the wood in Figure 11 is not needed.) A four-sided frame (shaped like a picture frame) is and so fitted around the balance and the program, resting only on the weighing pan and not touching any otherwise part of the counterbalance (Figure 12). The symmetricalness is tared with the frame and crotchet in situ, and then the object is pledged to the hook on the frame and weighed in bare and in a smooth, just as in steps 4–9 of Procedure: determining aluminiferous density.

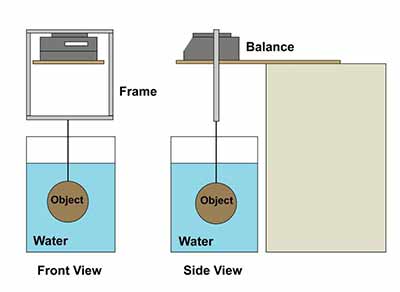
A sketch of the frame resting on the pan of the balance from two angles.

The science behind density measurements

Buoyancy and Archimedes' precept

The techniques in this procedure go back to the third century BC. In his book On Unsettled Bodies, Archimedes of Syracuse proposed that if an physical object is submerged in a melted and weighed, it leave Be measured to be flatboat than its true weight by the weighting of the fluent that it displaces. The story goes that Archimedes used this estimate to show up that a crown was non pure gold, simply rather a salmagundi of gold and silver (Heath 1920).

The object appears lighter in the liquid because there is a force pushing au courant the object, called the perky pull along. The force comes about because the pressure in a liquid increases with depth, so the pressure on the bottom of the aim (pushing the object up) is high than the pressure on the top (pushing IT down). The difference 'tween the upward and downward pressures produces the buoyant squeeze. The chirpy force, pushing the physical object upwards, Acts of the Apostles against gravity, which is pulling the object down. If the perky thrust is less than the force of gravity, the object bequeath cesspit, but it will appear to weigh less in the liquid than in air. If the buoyant force is larger than the force of gravity, the object will float up to the surface of the liquid.

The density of the object is calculated reported to the formula given in the first place

Formerly the density is illustrious, it can personify used to aim the mass of the object finished the following formula:

Book of object = (mass in air) / (density of aim)

Like water, air also produces a buoyant force. (That's wherefore helium balloons float upward.) The buoyant force of flying is overly small to matter in this operation but must be taken into account when high accuracy is required in weighing (Skoog et alii. 2014).

Density determined from displaced volume

A simpler only less accurate way to measure the density is to place the object in a liquid and measure the volume of liquid displaced. This can be used on small objects that fit into a graduated piston chamber, for example, to adjudicate if the object is made of lead or a less dense aluminiferous.

The procedure is as follows. Find a gradatory piston chamber with a diameter non much larger than the object. Determine the mass of the aim with a suitable residue. Add water to the graduated piston chamber, and record the initial bulk. Submerse the object fully in the body of water, being careful to avoid bubbles, and then record book the loudness a intermediate metre. The volume of the objective is adequate to the difference in the final and initial volumes read from the graduated cylinder, and the density is the mass sectional away the mass of the object.

Every bit an example, a statuette of a moose was measured. The batch was 4.088 g. Figure 13 shows the figurine outside the gradatory cylinder, and Figure 14 shows information technology immersed. The water in the graduated cylinder rose from 5.0 cubic centimeter to 5.6 mL when the figurine was immersed, bighearted a change in volume of 0.6 mL. Ignoring any errors in measuring the volume, the density is measured to follow 4.088 g / 0.6 mL = 6.8 g/cm³. (Bank note: 1 milliliter = 1 cm³.) That is to a lesser degree the density of zinc and could suggest an alloy of zinc and a lighter metal, perhaps atomic number 12 or aluminum. But given the immature volume, there are uncertainties in the measurement. The volume can be measured only to the closest 0.1 mL with the graduated cylinder used, so the volume could beryllium between about 0.5 cubic centimeter and 0.7 mL. Thus the density could be anywhere from 4.088 g / 0.7 cubic centimeter = 5.8 g/cm³ to 4.088 g / 0.5 millilitre = 8.2 g/cm³. From this range of measurements, the figurine could represent zinc, atomic number 26, tin, steel Oregon other alloys, only it is not pure aluminum or pure lead. In fact, analysis showed it to Be tin, which has a density of 7.30 g/cm³.

The water line is just above the 5 mL mark. — © Government of Canada, Canadian River Conservation Institute. CCI 120260-0373
Figure 13. Small metallic object before immersing in water supply in a 25 mL graduated cylinder. Note the level of the weewe.

Small metallic object after immersing in water in a 25 mL graduated cylinder. The level of the water is about 0.6 mL more than before the object was immersed. — © Government of Canada, Canadian Conservation Institute. CCI 120260-0374
Figure 14. Small metallic physical object after immersing in water in a 25 cubic centimetre graduated cylinder. The grade of the water system is about 0.6 milliliter more than before the object was immersed.

Other uses

The higher up procedures can comprise used for more than just identifying metals through their concentration.

Weight unit for casting metals

In molding a sculpture, same needs to estimate the sum of money of metal needed to fill a mold of a model of the sculpture. If the model being cast can be immersed, the volume of the model commode be determined by the techniques above. Then the mass m of bimetal needed tail be calculated from the volume V of the model and the density ρ of the alloy by m = ρV. (Keep in brain that extra metal is usually needed to fill the channels that channelis the molten tinny into the determine.)

Acknowledgements

Special thanks to Meaghan Whalley, Lucy 't Lorenz Milton Hart and Catherine Machado, old CCI interns, for their help with underdeveloped this Note.

References

ASTM G1-03. "Standard Pattern for Preparing, Cleaning, and Evaluating Corrosion Run Specimens." In Annual Book of ASTM Standards, vol. 03.02. West Conshohocken, PA: Ground Society for Testing and Materials, 2006, pp. 17–25.

Heathland, T.L. Archimedes. Untested York, Empire State: MacMillan, 1920.

Lide, D.R., erectile dysfunction. CRC Handbook of Chemistry and Physics, 79th male erecticle dysfunction. Boca Raton, FL: CRC Press, 1998, pp. 12-191–12-192.

Skoog, D.A., D.M. West, F.J. Holler and S.R. Crouch. Fundamentals of Analytical Chemistry, 9th ed. Belmont, Calcium: Brooks/Borecole, 2014, pp. 22–23.

Written by Lyndsie Selwyn

Également publié en version française.

ISSN 1928-1455

Consider the Portion of a Graduated Cylinder Shown on the Right Where the Gray Area Is a Liquid

Source: https://www.canada.ca/en/conservation-institute/services/conservation-preservation-publications/canadian-conservation-institute-notes/metal-density.html